论文阅读：A Cipher-Agnostic Neural Training Pipeline with Automated Finding of Good Input Differences

论文《A Cipher-Agnostic Neural Training Pipeline with Automated Finding of Good Input Differences》

文章主题是neural cryptanalysis （神经网络辅助的密码分析），回顾了现有的神经密码分析的成果，指出了在应用到新密码(speck32/64之外的)的困难。尤其是当前的方法在应对更大规模的密码时存在问题，并且在处理不同类型密码时也有局限性。论文的两个主要工作：

1. 提出了一种进化算法，用于搜索单密钥和相关密钥的输入差分。该算法使用了大分组的密码，并且减少了对机器学习的依赖，更多地关注于密码分析方法本身；
   • 为了训练准确率高的区分器，需要寻找适合的输入差分。该算法可以自动化搜索用于训练区分器的输入差分；
2. 提出了一个与密码结构无关的神经网络DBitNet，在多个密码上的表现优于现有的网络结构。
   • 对新的密码算法实施密钥恢复攻击时，不需要重新修改网络结构来适应不用的密码长度等；

背景知识

1. Simon32/64的轮函数

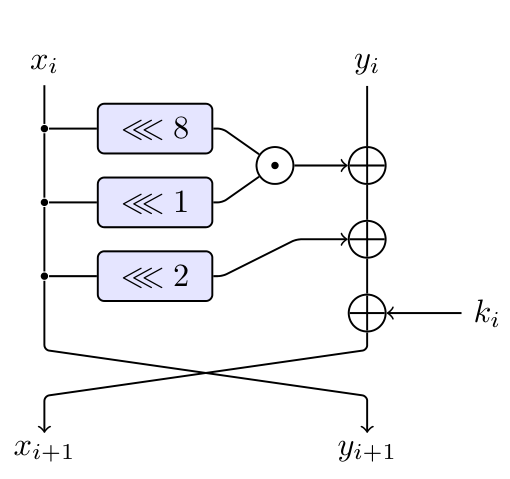Speck32/64的轮函数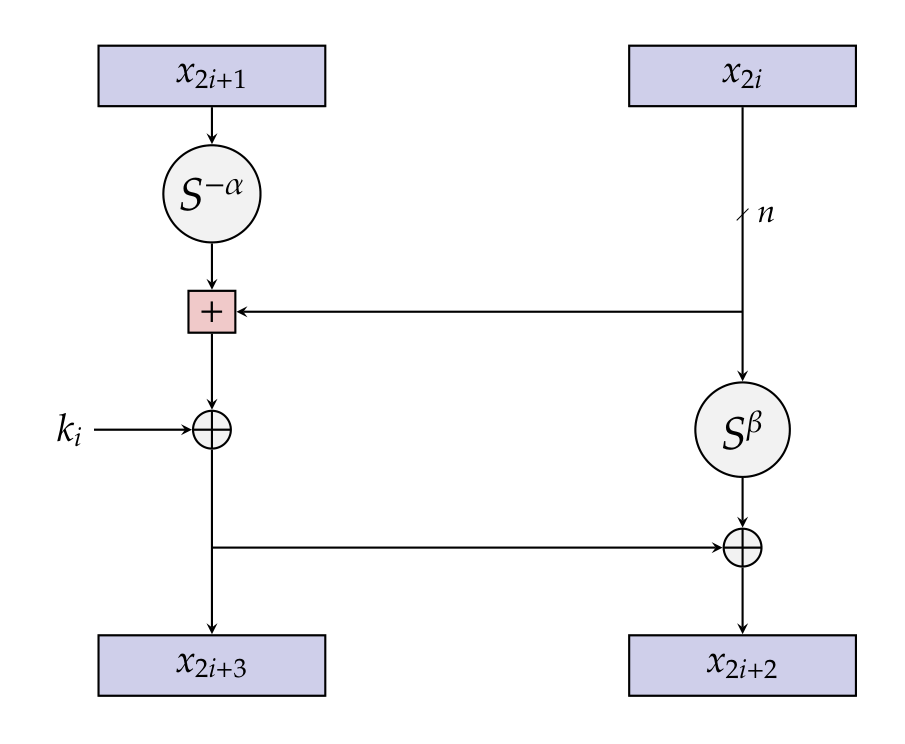

• Simon算法的参数一共有10个成员

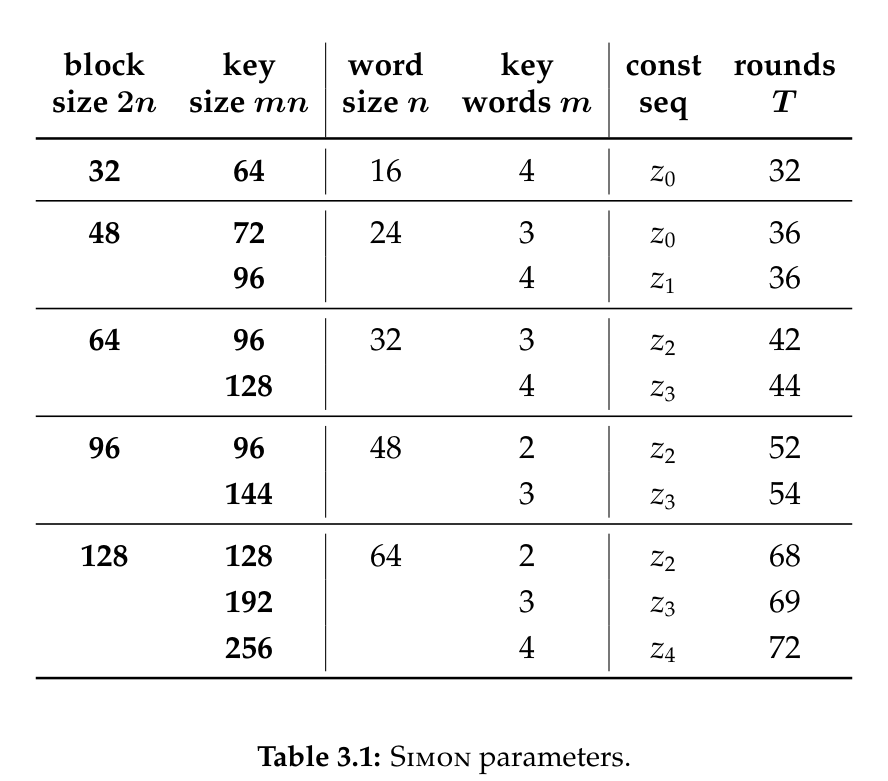验证向量：

2. 神经区分器： 充当传统差分攻击中的差分区分器，本质上是一个执行二分类任务的神经网络。

摘要

首先一起来读下摘要 > Abstract > Neural cryptanalysis is the study of cryptographic primitives through machine learning techniques. We review recent results in neural cryptanalysis, and identify the obstacles to its application to new, different primitives. As a response, we provide a generic tool for neural cryptanalysis, composed of two parts. The first part is an evolutionary algorithm for the search of single-key and related-key input differences that works well with neural distinguishers; this algorithm fixes scaling issues with Gohr’s initial approach and enables the search forlarger ciphers, while removing the dependency on machine learning, to focus on cryptanalytic methods. The second part is DBitNet, a neural distinguisher architecture agnostic to the structure of the cipher. We show that DBitNet outperforms state-of-the-art architectures on a range of instances. Using our tool, we improve on the state-of-the-art neural distinguishers for SPECK64, SPECK128, SIMON64, SIMON128 and GIMLI-PERMUTATION and provide new neural distinguishers for HIGHT, LEA, TEA, XTEA and PRESENT.

神经密码分析是一个通过机器学习技术来研究密码学原语的学科。本文回顾了最近在神经密码分析方面的研究成果，并指出其应用于新的(区别于sp32)、不同密码原语时遇到的障碍。对此，本文提供了一种通用的神经密码分析工具。该工具由两个部分组成：第一部分是一个进化算法，用于搜索适用于神经区分器的单密钥和相关密钥输入差分。该算法修复了Gohr最初方法中的扩展问题，并且可以用于更大规模的密码搜索，同时去除了对机器学习的依赖，重点关注密码分析方法。第二部分是一种与密码结构无关的神经区分器架构DBitNet，在多个密码上的表现优于当前最好的结果。基于以上工具，改进了SPECK64、SPECK128、SIMON64、SIMON128 和 GIMLI-PERMUTATION 的神经区分器， 并为HIGHT、LEA、TEA、XTEA 和 PRESENT 提供了新的神经区分器。

实验结果

区分器

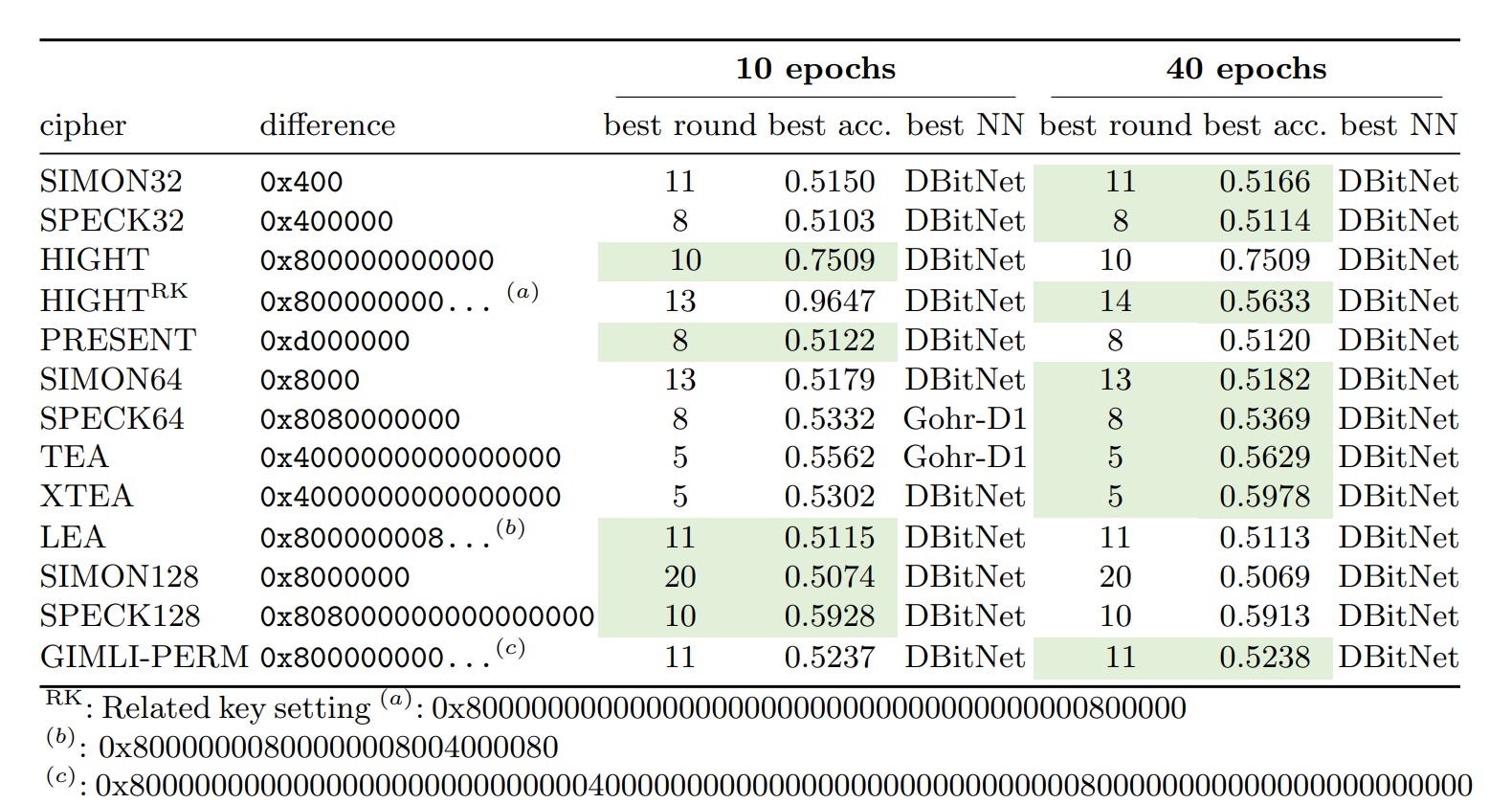
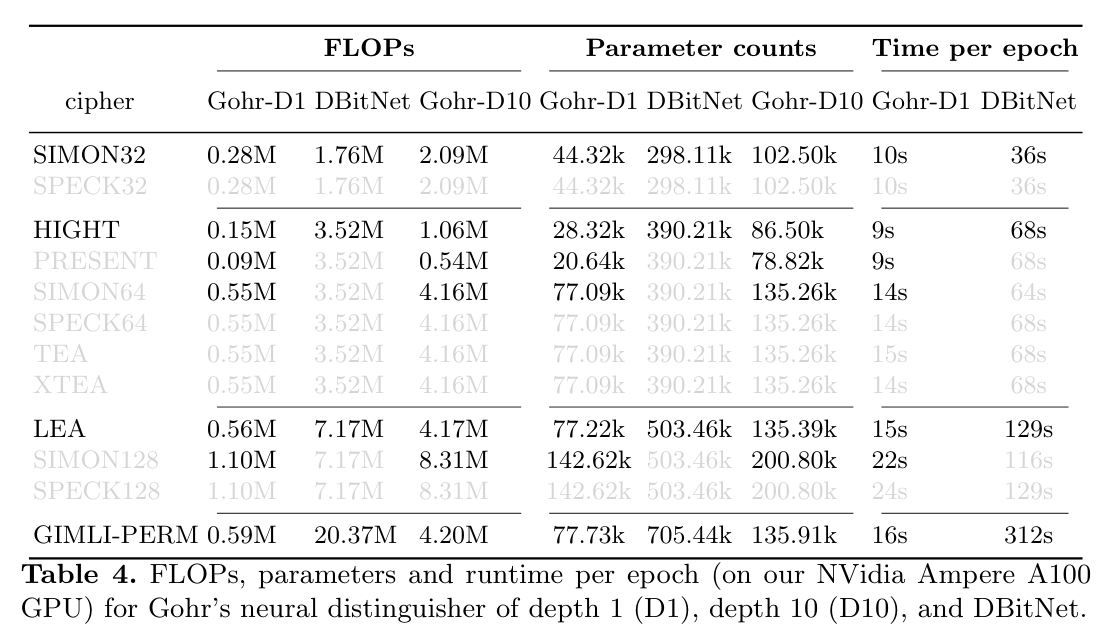
回顾Gohr的工作

神经网络可视化

自动搜索最优差分[岭回归]

• few-shot learning 没有先验人工知识的情况下推导出适用于神经区分器的好的输入差分

进化算法

• 偏差分数（bias score）对每个输入差分进行评分。该分数基于差分在经过多轮加密后对输出比特的影响进行计算，分数越高的差分意味着它能够更好地被神经网络捕捉。

• Bias score

• *

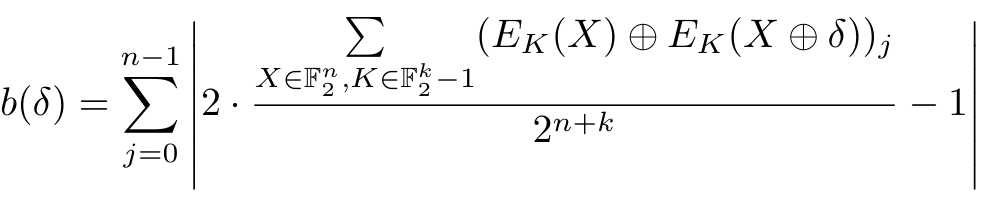
• Approximate bias score

• 

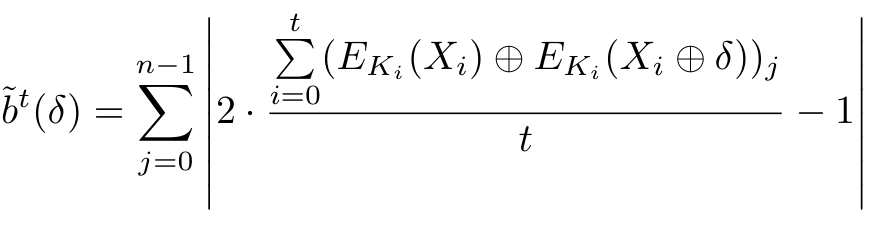
• 算法

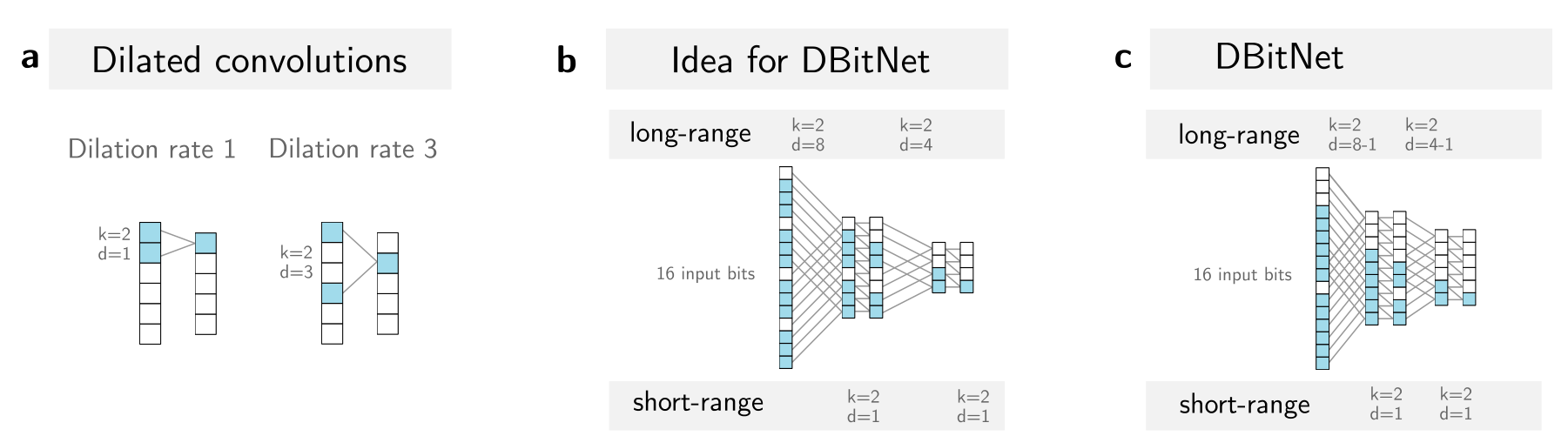
DBitNet

1. 对于新的密码，需要重新处理输入结构扩张卷积（dilated convolution) 扩张卷积通过增加卷积核的间距来学习输入数据中远距离和近距离的依赖关系，有效捕获输入比特位之间的长距离依赖，而不需要像 Gohr 的方法那样通过手动调整输入的重组方式来实现。DBitNet 设计了一个递增的卷积层，逐渐减少神经元的宽度，并同时增加卷积滤波器的数量，以确保网络能够有效学习到输入数据的复杂关系。

• Gohr ND 可视化
• DBitNet

import tensorflow as tf
    from tensorflow.keras.models import Model
    from tensorflow.keras.layers import Input, Conv1D, Dense, Dropout, Lambda, concatenate, BatchNormalization, Activation, Add
    from tensorflow.keras.regularizers import l2

def get_dilation_rates(input_size):
    """Helper function to determine the dilation rates of DBitNet given an input_size. """
    drs = []
    while input_size >= 8:
        drs.append(int(input_size / 2 - 1))
        input_size = input_size // 2

    return drs

def make_model(input_size=64, n_filters=32, n_add_filters=16):
    """Create a DBITNet model.

    :param input_size: e.g. for SPECK32/64 the input_size is 64 bit.
    :return: DBitNet model.
    """
    # determine the dilation rates from the given input size
    dilation_rates = get_dilation_rates(input_size)

    # prediction head parameters (similar to Gohr)
    d1 = 256 # TODO this can likely be reduced to 64.
    d2 = 64
    reg_param = 1e-5

    # define the input shape
    inputs = Input(shape=(input_size, 1))
    x = inputs

    # normalize the input data to a range of [-1, 1]:
    x = tf.subtract(x, 0.5)
    x = tf.divide(x, 0.5)

    for dilation_rate in dilation_rates:
        ### wide-narrow blocks
        x = Conv1D(filters=n_filters,
                   kernel_size=2,
                   padding='valid',
                   dilation_rate=dilation_rate,
                   strides=1,
                   activation='relu')(x)
        x = BatchNormalization()(x)
        x_skip = x
        x = Conv1D(filters=n_filters,
                   kernel_size=2,
                   padding='causal',
                   dilation_rate=1,
                   activation='relu')(x)
        x = Add()([x, x_skip])
        x = BatchNormalization()(x)

        n_filters += n_add_filters

    ### prediction head
    out = tf.keras.layers.Flatten()(x)

    dense0 = Dense(d1, kernel_regularizer=l2(reg_param))(out);
    dense0 = BatchNormalization()(dense0);
    dense0 = Activation('relu')(dense0);
    dense1 = Dense(d1, kernel_regularizer=l2(reg_param))(dense0);
    dense1 = BatchNormalization()(dense1);
    dense1 = Activation('relu')(dense1);
    dense2 = Dense(d2, kernel_regularizer=l2(reg_param))(dense1);
    dense2 = BatchNormalization()(dense2);
    dense2 = Activation('relu')(dense2);
    out = Dense(1, activation='sigmoid', kernel_regularizer=l2(reg_param))(dense2)

    model = Model(inputs, out)

    return model

总结

论文主要的工作在于解决了两个痛点：

1. 寻找最佳的输入差分来进行神经网络的训练；对于全密文的区分器，确定区分器的输入差分，可以从传统结果中进行寻找；或者直接简单粗暴地遍历所有的单差分。文中使用一种进化算法，来搜索适用于神经区分器的单密钥和相关密钥输入差分。
2. 自动适应新的算法结构；目前大部分神经区分器是针对Speck32/64进行训练， 当密码结构改变时，例如目标密码改为Speck64/96，那么原来神经网络的输入结构需要进行相应的改变。文中引入扩张卷积来自动化的适应密码结构，并且该结构能够学习到更多信息。

但实际上真的解决问题了吗? 论文中没有论证进化算法搜索到的输入差分是最优的，实际上很可能是次优解，但对于快速寻找输入差分也是OK的。另一方面，正如论文题目：